9461번: 파도반 수열
문제 오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 �
www.acmicpc.net
문제
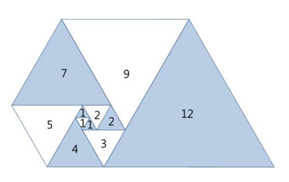
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)
출력
각 테스트 케이스마다 P(N)을 출력.
풀이
그림을 보면 이전 정삼각형들의 변을 더하는 식이라 간단하다.
첫 10개의 숫자들을 예시로 들면
P(5)까지는 주어진 값으로 초기화 시켜주고
P(6) = 3 = P(1) + P(5)
P(7) = 4 = P(2) + P(6)
P(8) = 5 = P(3) + P(7)
P(9) = 7 = P(4) + P(8)
P(10) = 9 = P(5) + P(9) 임을 알 수 있다.
따라서 점화식은 P(N) = P(N-1) + P(N-5) (N>5) 이다.
public class bj9461 {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner s = new Scanner(System.in);
long P[] = new long[101]; // int형 주면 틀림
P[0] = 0;
P[1] = 1;
P[2] = 1;
P[3] = 1;
P[4] = 2;
P[5] = 2;
for(int i=6;i<101;i++) {
P[i] = P[i-1]+P[i-5];
}
int T = s.nextInt(); // 테스트 케이스의 개수 T
for(int t=0;t<T;t++) {
int n = s.nextInt(); // N 입력받음
System.out.println(P[n]);
}
s.close();
}
}
'Algorithm & Data Structure > 백준' 카테고리의 다른 글
| [JAVA] 백준 14501번 : 퇴사 (0) | 2020.05.16 |
|---|---|
| [JAVA] 백준 1932번 : 정수 삼각형 (0) | 2020.05.15 |
| [JAVA] 백준 2293번 : 동전 1 (0) | 2020.05.08 |
| [JAVA] 백준 11726번 : 2Xn 타일링 (0) | 2020.05.08 |
| [JAVA] 백준 2225번 : 합분해 (2) | 2020.05.08 |
![[JAVA] 백준 9461번 : 파도반 수열](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fdr6hHW%2FbtqDZNplahG%2FAAAAAAAAAAAAAAAAAAAAAG1sVdzYHvd39mgzuRebCXf43Fzp8SeajapFq-AoSFdG%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DJrCYKdRw2QItrDW09JICP2HkC0s%253D)