https://programmers.co.kr/learn/courses/30/lessons/62048
코딩테스트 연습 - 멀쩡한 사각형
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을
programmers.co.kr
풀이
대각선으로 잘리는 사각형 패턴은, 최대 공약수로 나눈 작은 사각형만큼 반복한다.
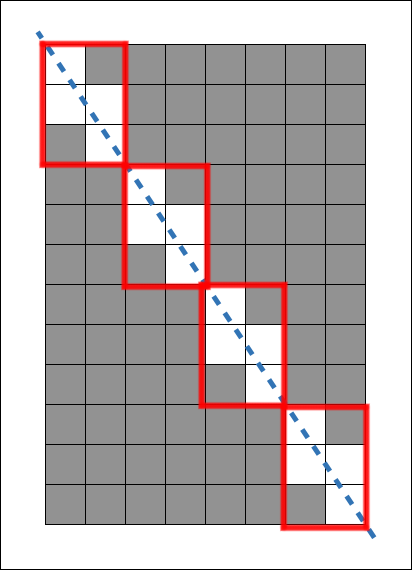
예를 들어 가로 8, 세로 12인 직사각형이면 가로세로를 각각 4(8과 12의 최대공약수)로 나눈 가로 2, 세로 3인 직사각형이 반복됨을 알 수 있다. 그 중 가운데에서 대각선으로 잘리는 사각형은 최대공약수인 4번 반복된다. 즉, 가로 2 세로 3인 직사각형에서 못쓰는 사각형의 개수에 최대공약수인 4를 곱하면 가로 8 세로 12인 직사각형에서 못쓰는 사각형의 개수 16개를 구할 수 있게 된다.
(직사각형에서 못쓰는 사각형의 개수) = (최소 사각형에서 못쓰는 사각형의 개수) * (최대공약수)
사각형에서 대각선으로 잘려 못쓰는 사각형의 개수를 구하기 위해 밑의 예시를 들어보자.
| 가로 | 세로 | 못쓰는 사각형 개수 |
| 1 | 1 | 1 |
| 1 | 2 | 2 |
| 1 | 3 | 3 |
| 2 | 3 | 4 |
| 2 | 5 | 6 |
위에서 (최소 사각형에서 못쓰는 사각형의 개수) = (가로)+(세로)-1 의 패턴을 발견할 수 있다.
최종적으로 공식은 다음과 같다.
(가로 w, 세로 h 직사각형에서 못쓰는 사각형의 개수) = (w/gcd)+(h/gcd)-1 * (gcd) (*gcd : w, h의 최대공약수)
공식을 적용해 코드를 작성한 것이다.
class Solution {
public long solution(int w, int h) {
long answer = 1;
int gcd = gcd(Math.max(w,h),Math.min(w,h)); // 최대공약수
return (long)(w*h-(w+h-gcd));
}
// 최대공약수 구하는 함수
int gcd(int a, int b){
if(b==0) return a;
return gcd(b,a%b);
}
}'Algorithm & Data Structure > 프로그래머스' 카테고리의 다른 글
| [Java] 프로그래머스 Lv.2 > 전화번호 목록 (0) | 2022.03.04 |
|---|---|
| [Java] 프로그래머스 Lv.2 > 124 나라의 숫자 (0) | 2022.03.04 |
| [Java] 프로그래머스 Lv.2 > 가장 큰 수 (0) | 2022.02.28 |
| [Java] 프로그래머스 Lv.2 > 큰 수 만들기 (0) | 2022.02.28 |
| [Java] 프로그래머스 Lv.2 > 기능개발 (0) | 2022.02.28 |
![[Java] 프로그래머스 Lv.2 > 멀쩡한 사각형](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FcuSo7k%2FbtruDCwvgnE%2FAAAAAAAAAAAAAAAAAAAAAJOn90Rsi4ENLEMsNfNgIaUqYpEIbR_oaxoafHqpjP8o%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DtSP6MUXgze3jwY%252BEtXcyjZihgVc%253D)